Page 89 - Una innovación a la mecánica cuántica

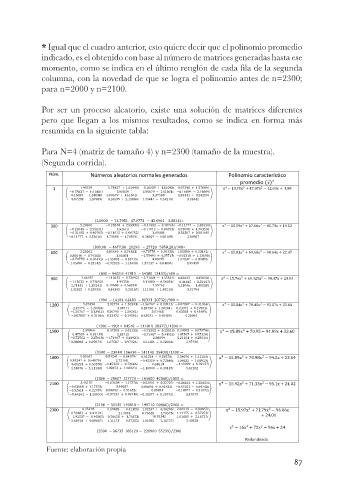
* Igual que el cuadro anterior, esto quiere decir que el polinomio promedio
indicado, es el obtenido con base al número de matrices generadas hasta ese
momento, como se indica en el último renglón de cada fila de la segunda
columna, con la novedad de que se logra el polinomio antes de n=2300;
para n=2000 y n=2100.

Por ser un proceso aleatorio, existe una solución de matrices diferentes
pero que llegan a los mismos resultados, como se indica en forma más
resumida en la siguiente tabla:

Para N=4 (matriz de tamaño 4) y n=2300 (tamaño de la muestra).
(Segunda corrida).
Núm. Números aleatorios normales generados Polinomio característico
promedio ( ̅)
∗
1 1.98729 −0.78427 + 1.61441 −0.16039 + 1.61088 0.07298 + 1.37089 x ! − 13.70x " + 47.07x # − 42.69x + 3.88
! −0.78427 − 1.61441 5.00834 2.00679 − 1.61601 −0.16699 − 2.19869 1
−0.16039 − 1.61088 2.00679 + 1.61601 3.37508 1.33441 + 0.24219
0.07298 − 1.37089 −0.16699 + 2.19869 1.33441 − 0.24219 3.33442

(1.0000 − 13.7051 47.0773 − 42.6961 3.8834)=
300 5.29300 −0.22048 + 2.55831 −0.31982 − 0.40765 −0.11777 − 2.33636 x ! − 15.59x " + 67.66x # − 85.73x + 19.52
−0.22048 − 2.55831 5.52613 −0.11012 − 0.06752 1.73098 + 1.70359 1
!
−0.31982 + 0.40765 −0.11012 + 0.06752 3.69386 0.34307 + 0.58168
−0.11777 + 2.33636 1.73098 − 1.70359 0.34307 − 0.58168 3.59867
(300.00 − 4677.80 20298 − 25720 5858.20)/300=
600 2.25061 0.85640 + 0.74363 −0.70778 − 0.36331 1.05890 + 0.23142 x ! − 15.81x " + 69.68x # − 90.64x + 22.47
! 0.85640 − 0.74363 2.05601 −1.55493 + 0.35715 −0.92318 + 1.13698 1
−0.70778 + 0.36331 −1.55493 − 0.35715 4.96695 1.37137 − 0.84894
1.05890 − 0.23142 −0.92318 − 1.13698 1.37137 + 0.84894 3.99490
(600 − 9488.9 41811 − 54388 13483)/600 =
900 3.66957 −1.12032 − 0.73092 −2.71441 − 1.35541 1.32625 − 0.35033 x ! − 15.76x " + 69.425x # − 90.37x + 23.03
−1.12032 + 0.73092 1.99350 0.11080 − 0.56034 −0.34345 + 0.50167 1
!
−2.71441 + 1.35541 0.11080 + 0.56034 7.51762 1.11096 − 1.48218
1.32625 + 0.35033 −0.34345 − 0.50167 1.11096 + 1.48218 3.31794
(900 − 14184 62483 − 81333 20732)/900 =
1200 5.87498 2.32776 + 1.20934 −1.56767 + 0.13412 −0.07887 − 0.31064 x ! − 15.84x " + 70.45x # − 93.17x + 23.64
2.32776 − 1.20934 3.08711 0.20790 + 1.20201 0.23372 + 0.19561 1
!
−1.56767 − 0.13412 0.20790 − 1.20201 3.01468 0.63031 + 0.45489
−0.07887 + 0.31064 0.23372 − 0.19561 0.63031 − 0.45489 0.28091
(1200 − 19014 84540 − 111810 28377)/1200 =
1500 1.69866 0.47593 − 0.02135 −0.72502 + 0.25618 0.38008 − 0.07074 x − 15.89x + 70.95 − 94.09x + 23.60
!
"
0.47593 + 0.02135
! 2.83715 −1.71967 − 0.44923 1.07587 + 0.97324 1
−0.72502 − 0.25618 −1.71967 + 0.44923 2.88099 0.21184 + 0.28016
0.38008 + 0.07074 1.07587 − 0.97324 0.21184 − 0.28016 2.97186
(1500 − 23848 106430 − 141140 35408)/1500 =
1800 5.03667 0.83241 − 0.64079 0.61224 − 0.53578 2.54076 + 1.11183 x − 15.89x + 70.98x − 94.2x + 23.64
"
#
!
0.83241 + 0.64079 2.72168 −0.45329 + 0.72646 1.09632 − 1.08923 1
!
0.61224 + 0.53578 −0.45329 − 0.72646 0.84614 −1.10909 + 0.39137
2.54076 − 1.11183 1.09632 + 1.08923 −1.10909 − 0.39137 5.61262
(1800 − 28607 127770 − 169600 42568)/1800 =
2100 3.45187 −0.63608 − 1.17378 −0.52611 + 0.22707 −0.46161 + 1.28653 x − 15.92x + 71.33x − 95.1x + 24.02
#
!
"
−0.63608 + 1.17378 3.49087 0.08892 + 0.91632 −0.97251 − 0.69748 1
!
−0.52611 − 0.22707 0.08892 − 0.91632 0.89841 −0.18877 − 0.31072
−0.46161 − 1.28653 −0.97251 + 0.69748 −0.18877 + 0.31072 1.47878
(2100 − 33435 149810 − 199710 50460)/2100 =
2300 4.35218 0.59483 − 0.41121 1.92237 + 0.40205 2.66918 − 0.80667 x − 15.97x + 71.79x − 96.06x
#
!
"
0.59483 + 0.41121 1
! 2.14048 0.76628 − 1.70573 1.11175 + 0.57253 + 24.01
1.92237 − 0.40205 0.76628 + 1.70573 10.92342 1.01685 + 2.16727
2.66918 + 0.80667 1.11175 − 0.57253 1.01685 − 2.16727 3.43428
x − 16x + 72x − 96x + 24
!
#
"
(2300 − 36735 165120 − 220960 55239)/2300

redondeado

Fuente: elaboración propia
87