Page 202 - Una innovación a la mecánica cuántica

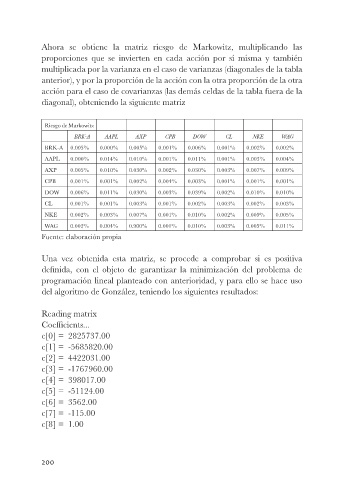
Ahora se obtiene la matriz riesgo de Markowitz, multiplicando las
proporciones que se invierten en cada acción por sí misma y también
multiplicada por la varianza en el caso de varianzas (diagonales de la tabla
anterior), y por la proporción de la acción con la otra proporción de la otra
acción para el caso de covarianzas (las demás celdas de la tabla fuera de la
diagonal), obteniendo la siguiente matriz

Riesgo de Markowitz
BRK-A AAPL AXP CPB DOW CL NKE WAG
BRK-A 0.005% 0.000% 0.005% 0.001% 0.006% 0.001% 0.002% 0.002%
AAPL 0.000% 0.014% 0.010% 0.001% 0.011% 0.001% 0.003% 0.004%
AXP 0.005% 0.010% 0.030% 0.002% 0.030% 0.003% 0.007% 0.009%
CPB 0.001% 0.001% 0.002% 0.004% 0.003% 0.001% 0.001% 0.001%
DOW 0.006% 0.011% 0.030% 0.003% 0.039% 0.002% 0.010% 0.010%
CL 0.001% 0.001% 0.003% 0.001% 0.002% 0.003% 0.002% 0.003%
NKE 0.002% 0.003% 0.007% 0.001% 0.010% 0.002% 0.009% 0.005%
WAG 0.002% 0.004% 0.900% 0.001% 0.010% 0.003% 0.005% 0.011%
Fuente: elaboración propia

Una vez obtenida esta matriz, se procede a comprobar si es positiva
definida, con el objeto de garantizar la minimización del problema de
programación lineal planteado con anterioridad, y para ello se hace uso
del algoritmo de González, teniendo los siguientes resultados:

Reading matrix
Coefficients...
c[0] = 2825737.00
c[1] = -5685820.00
c[2] = 4422031.00
c[3] = -1767960.00
c[4] = 398017.00
c[5] = -51124.00
c[6] = 3562.00
c[7] = -115.00
c[8] = 1.00

200